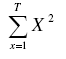Difference between revisions of "Checkerboard Squares POW"

Revision as of 22:57, 21 June 2007

IAG 1H POW # 3: Checkerboard Squares

1. Problem Statement: You need to find the number of squares in an 8 by 8 square. You also need to find a pattern for finding the number of squares in any size square.

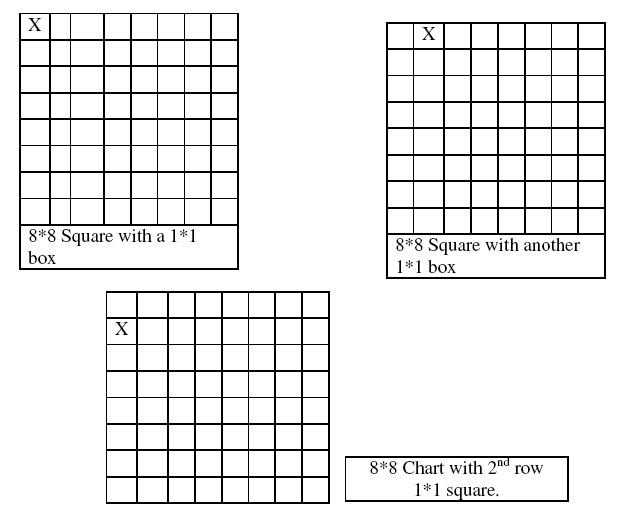
2. Process: Well to sole this problem, I first made and 8*8 chart.

I then found a 1 by 1 square in the box. I marked the squares in the square in the square with X’s. I can also start one on the 2nd row.

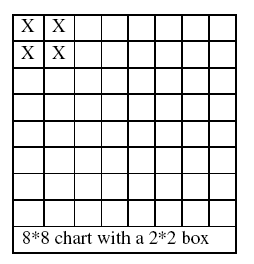
I then figured I could do this for all 64 squares. I then moved onto 2*2 squares.

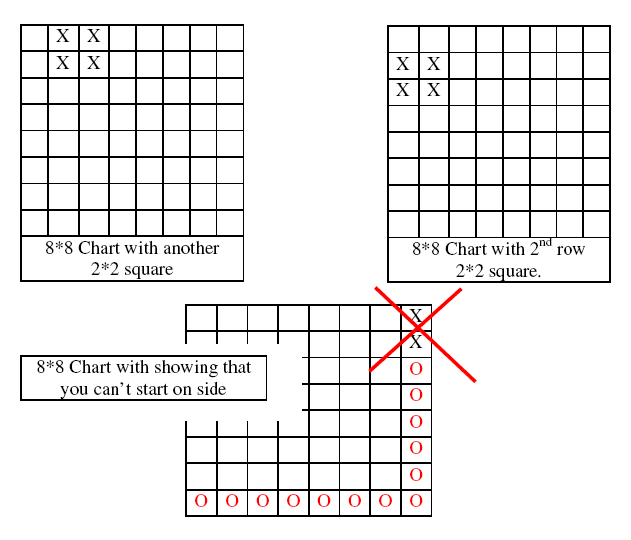
I then did another 2 by 2 chart. I can also have squares overlap others. I then figured out that I could not start a 2*2 square of the last row and column of the chart. I could fit only 7 rows by 7 columns of 2*2 squares, for a total of 49 squares.

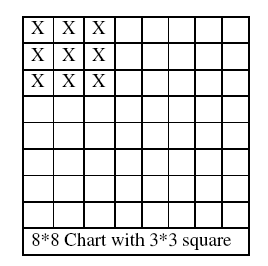
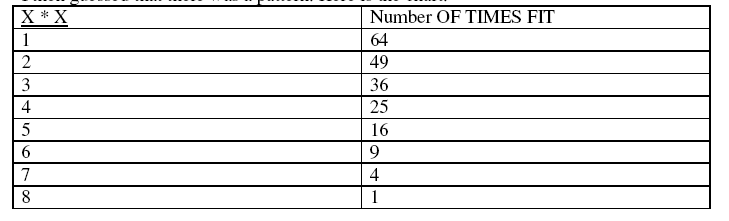
I then repeated that 1 more time to make sure. I am guessing that there will be 36, 3*3 squares in this 8*8 square.

I then guessed that there was a pattern. Here is the chart.

At first, I forgot the 4*4 square was 25, so my chart was messed up, but then I corrected my mistake. I added up the number of squares in the 8*8 square, to get …

3. Solution: …204 squares are in an 8*8 square. I also assumed a pattern out of this. If you subtract the length of the number of squares you want to find by the length of the big, total square, and cube that. Here it is spelled out. X=length of smaller cube (as above), T=length of 1 side of the big cube (above it was 8) (T-X)2

Example for finding the number of 7*7 cubes in a 15*15 cube, you do (15-7)2 or 82 or 64. You will need to use all of the X’s from 1 to 15. For example for 15 do

4. Extension: Not necessary to do.

5. Evaluation: Not necessary to do.