Difference between revisions of "Sticky Gum Problem POW"
From ThePlaz.com
(post) |
m (heading) |
||
| Line 58: | Line 58: | ||
[[Image:Sticky Gum Problem Diagram 6.png]] | [[Image:Sticky Gum Problem Diagram 6.png]] | ||
| − | + | ''3. Solution (Ultimate Goal): '' | |
Let me make another chart. I have included 1 color and 1 kid for comparison. | Let me make another chart. I have included 1 color and 1 kid for comparison. | ||
Revision as of 01:25, 22 June 2007
IAG 1H POW # 4: A Sticky Gum Problem
A Microsoft Word version of this work is available here: Image:A_Sticky_Gum_Problem.doc
![]() A PDF version of this work is available here: Image:A_Sticky_Gum_Problem.pdf
A PDF version of this work is available here: Image:A_Sticky_Gum_Problem.pdf
1. Problem Statement: Not necessary to do.
2. Process and answers to problems 1,2 & 3: 1. (2 colors, 2 people) Ms. Hernandez can only spend 3 cents, because on her first cent, she can get a white or a red gumball. On her second turn, she can also only get a red or white gumball. Now she can only have 4 combinations: Red and White Gumballs; Red and Red Gumballs; White and White Gumballs; White and Red Gumballs. With 2 of these possible combinations, she already has her goal of having 2 of the same color gumballs. On her third try, she gets another red or white gumball. Whatever the color, she already has one of them, which makes 2 of the same color.
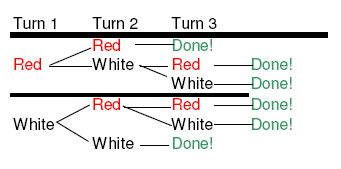
2. (3 colors, 2 people) Ms. Hernandez now finds a machine that has 3 colors in it. The most that she will need to spend to get 2 of the same color is 4 cents. To find all of the possible strategies, look at the chart:
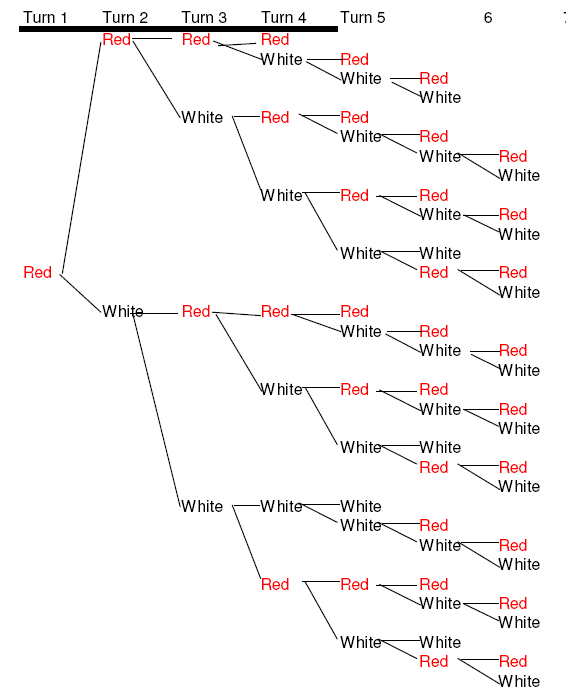
3. (3 colors, 3 people) It will take 7 cents to get 3 of the same color, as there are 108 possible combinations. Here is a chart showing the 1st third of them (if the first color is red)
I will now make a chart showing my findings so far.
| Colors | Kids | Max Spend | Combos |
| 2 | 2 | 3 cents | 6 |
| 3 | 2 | 4 cents | 33 |
| 3 | 3 | 7 cents | 108 |
Now I will make up some problems to help fill in the chart some more.
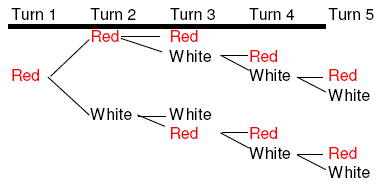
4. (2 colors, 3 kids) This chart shows the first half of needing 3 of the same color, with only 2 colors. It will take 5 cents and there are 16 combinations.
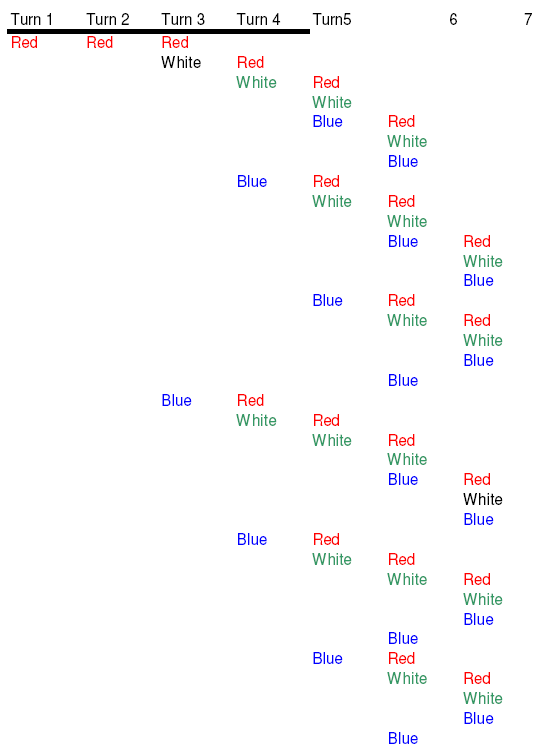
5. (2 colors, 4 kids) This shows the first half of getting 4 of 1 color and having 2 colors. You need 7 cents, and there are 68 combos.
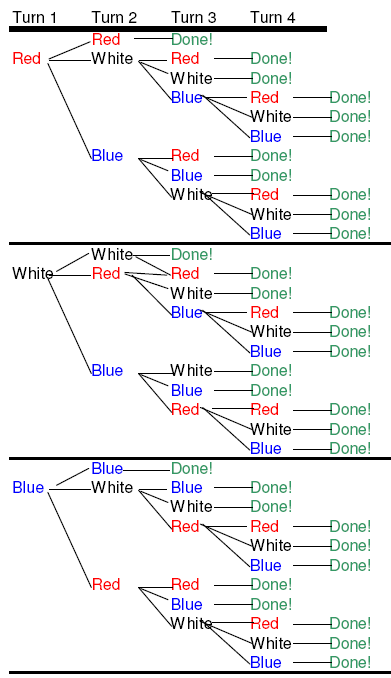
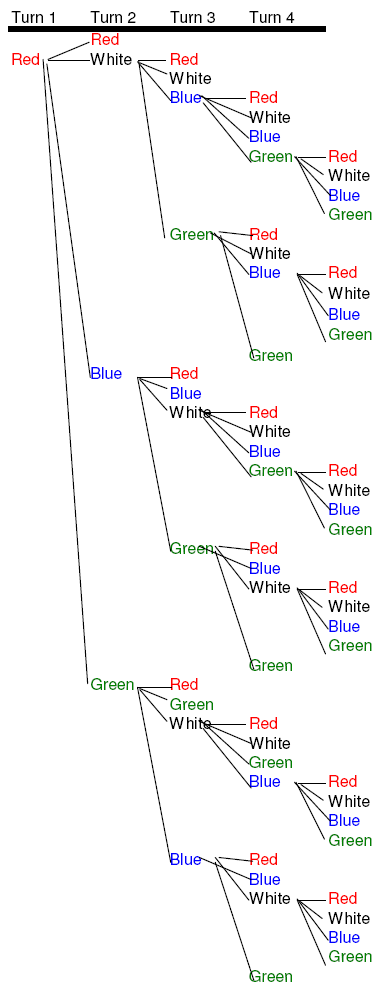
6. (4 colors, 2 kids) This shows the first quarter of the chart, when you need 2 of the same, and there are 4 colors. You need 5 turns to get 4 of the same, and there are 200 combinations.
3. Solution (Ultimate Goal):
Let me make another chart. I have included 1 color and 1 kid for comparison.
| Colors | Kids | Max Spend | Combos |
| 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 |
| 2 | 1 | 1 | 2 |
| 2 | 2 | 3 cents | 6 |
| 2 | 3 | 5 | 16 |
| 2 | 4 | 7 | 68 |
| 3 | 2 | 4 cents | 33 |
| 3 | 3 | 7 cents | 108 |
| 4 | 2 | 5 | 200 |
Overall, I have found that number of colors is ultimately responsible for combinations, but the number of kids is ultimately responsible for the maximum, you spend. Here is something interesting:
| Colors | Kids | Max Spend |
| 2 | 2 | 3 |
| 3 | 4 | |
| 4 | 5 |
When you have 2 kids max spend is equal to number of colors plus 1. What about having 3 kids:
| Colors | Kids | Max Spend |
| 2 | 3 | 5 |
| 3 | 4 |
This chart shows so far that when you add a color, the max that you spend, goes down.
When you start adding a color, the number of cents goes down; when you then keep adding people, the number of cents goes up.
I have also found that this works: [(# of colors) * (# of kids)] - [(# of colors) – 1]
4. Extension: Not necessary to do.
5. Evaluation: Not necessary to do.