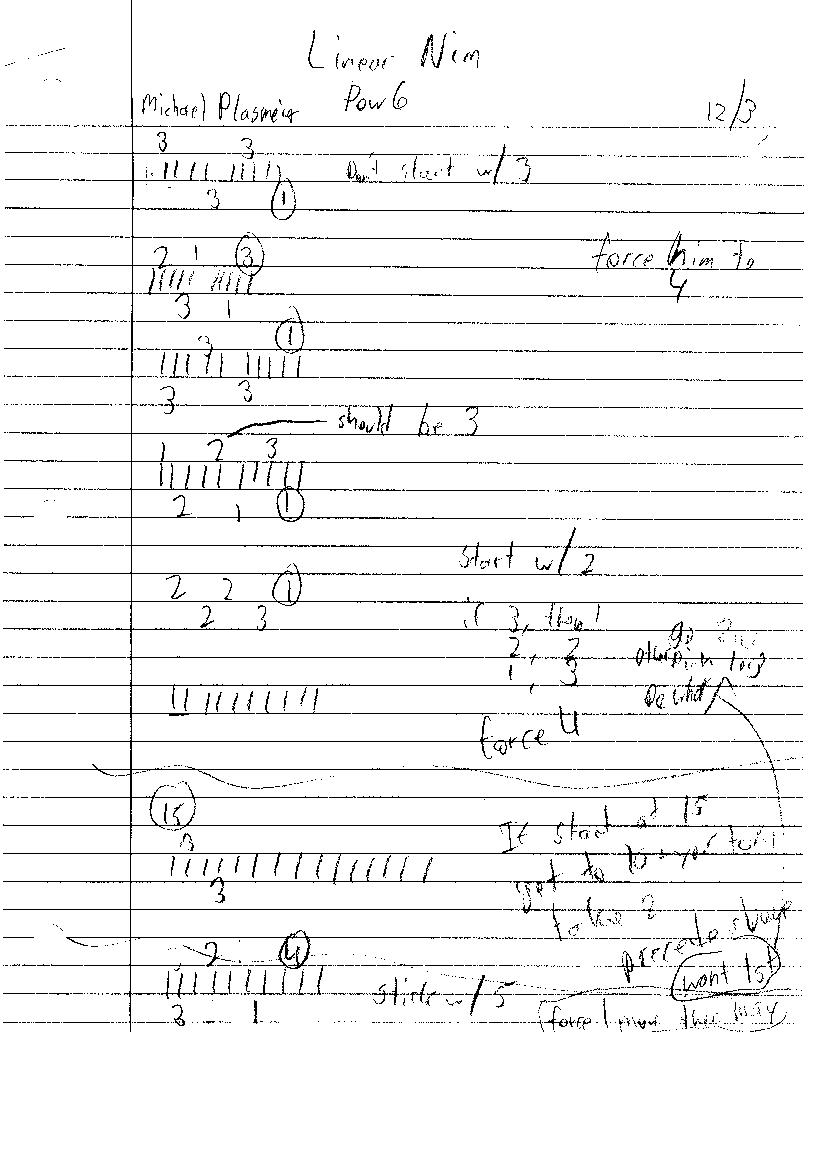Difference between revisions of "Linear Nim POW"
From ThePlaz.com
(post) |
(pow link) |
||
| Line 1: | Line 1: | ||
| − | <big>'''[[IAG 1H]] POW <nowiki>#</nowiki> 6: Linear Nim'''</big> | + | <big>'''[[IAG 1H]] [[POW]] <nowiki>#</nowiki> 6: Linear Nim'''</big> |
{{Word|Image:Linear_Nim.doc}} | {{Word|Image:Linear_Nim.doc}} | ||
Revision as of 02:34, 22 June 2007
A Microsoft Word version of this work is available here: Image:Linear_Nim.doc
![]() A PDF version of this work is available here: Image:Linear Nim.pdf
A PDF version of this work is available here: Image:Linear Nim.pdf
Contents |
Instructions
Problem Statement
Not necessary to do.
Process (Playing)
I started playing Linear Nim with Michael Lewis. We started out just playing to try and find strategies. Our tallies are recorded below:
On my first try, I played going first and picking 3. Bad idea, I thought at first, I would always loose, but now I am thinking differently. Of course if the other person picks 3, I am left with 4. I later found out that was a bad idea. Picking 3 first is a bad idea because if the other player picks 3, your stuck with 4.
On my 2nd try, I started first at 2 and won. Later on, I found out that I should start with 2 going first. I figured out that I should stick my opponent with 4, and later I found out that it is equal to (maximum per turn)+1. This is sort of a interim goal where if you meet this goal you will win. I think you are able to think easier when you are dealing with less numbers. I won this game by playing the strategy mentioned in the solution.
On the 3rd try, I let my opponent go first. He picked 3 which was the mistake I made on my 1st turn. I ended up winning.
On the fourth try, I tried to pick 1 first. I lost by being stuck with 4. I could have won by watching more closely. If my opponent picks 1 on his first turn there are 8 lines left. If I pick 1, my opponent picks 1, I can pick 1, 2, or 3. Either way my opponent picks the opposite (you 1-he 3) or [(maximum per turn)-(his pick)+1] and it’s my choice with 4 left. He wins. If he picks 2, I can pick 3, and he picks with 4 and looses. If he picks 3, then I can pick 2, and leave him with 4. Therefore, picking 1 first lets your opponent control your fate.
The fifth time around I developed the winning strategy. See below.
I did not do anymore playing where I don’t go first, because I found my answer.
Work
Solution (of original)
I found out in my 5th term the winning strategy for the original game. If I went first, and picked 2, I could win. If my opponent picked 3, thin I would pick 1 on my next term. There would be 4 left and it would be his turn. If it’s your turn and you have 4 (maximum per turn)+1) left, you lose. Now when I picked 2 first, and my opponent picks 2, I would take 2 also to leave him with 4. If he takes 1, I take 3 and He is again left with 4. This is my strategy.
If the other person goes first, hope they won’t pick 2, if so, your done. If he picks 1 first, pick 2, or 3 and you might lose. If he picks 3, pick 3 and force him with 4.
Extension (Generalizations)
I am also seeing a pattern that leaving him with 4 [(maximum per turn)+1] requires I can also leave him with 8, which happens to be [2x(maximum per turn+1)] When I start at 10, I need to take 2 to get him to [2x(maximum per turn+1)]. I did not know that at the time, so we tried playing with 15 marks and keeping 3 at a time. I found that if you got the game down to 10 and your turn, it is just like playing the original game. I now also know that if I got him down to picking from 8 [2x(maximum per turn+1)] and my turn, I could also win. I suppose this will also work with all variations of X: [X*(maximum per turn+1)] in all variations of liner nim. I can also try and get him to 12 [3x(maximum per turn+1)], by going first and taking 3. I can now know that if I can go first, I will always win, unless [X*(maximum per turn+1)] is the starting number, where I would want him to go first.. This is because I can always take (initial number)-[X*(maximum per turn+1)], and catch him in a loop picking the opposite of what he picks, which equals, [(maximum per turn)-(his pick)+1].
I found out that trapping people at 4 was the same as (maximum per turn)+1 when I to increased the maximum per turn to 4 and played with the initial number of 10. I ended up winning, however it would have been better to have known the strategy above.
Faux Program
If initial number equals [X*(maximum per turn+1)];
Then
Label A
Have Partner Go
Take (maximum per turn)-(his pick)+1
Goto A
Else
Go First
Take (initial number)-[X*(maximum per turn+1)
Have Partner Go
Take (maximum per turn)-(his pick)+1
Goto A
During Problem: X is equal to the number closest to < (initial number)
Evaluation
Not necessary to do.