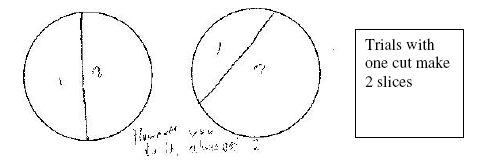Cutting the Pie POW

IAG 1H POW # 17: Cutting the Pie

A Microsoft Word version of this work is available here: Image:Cutting the Pie.doc

A PDF version of this work is available here: Image:Cutting the Pie.pdf

Circles

Circles to practice and work on:

A PDF version of this work is available here: Image:Circles.pdf

Problem Statement

Not necessary to do.

Process

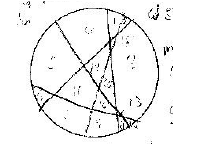
I first started out by printing out 3 sheets of circles that I could work on. I started from the beginning by making one cut. I tried again, like I thought, I could only make 2 pieces. Below, are my trials and my notes on my reasoning. I will include more of these where needed.

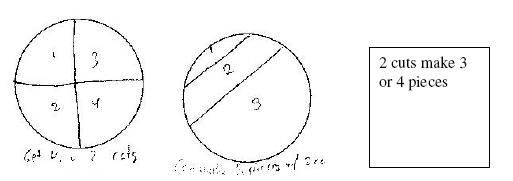
Next, I made 2 cuts. The first time, I cut all of the pieces into fourths, and got four pieces. I then found that I could also make 3 pieces with 2 cuts. I noticed that when I made 4 pieces, the 2 lines intercepted, but when I made 3 pieces, the lines did not intercept.

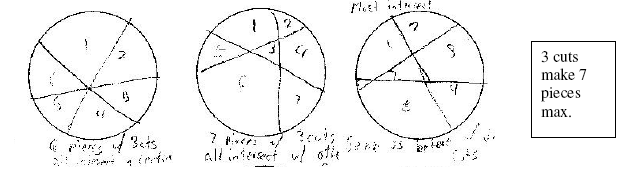
I noticed from the table on pg. 421 that 4 was the most I could make with 2 cuts, so I moved on to 3 cuts. I tried to cut the pie into sixths. I counted 6 pieces. According to the chart, I could make 7 pieces max. I also noticed in the picture on p. 420, that if all 3 cuts intersect in 1 place, 6 pieces is the most you can make. I decided to make a pie like the one on the right on pg. 420. I counted 7 pieces. I then noticed a few key points from this diagram. Every line intersects with the other 2 lines but each intersects in a different place, leaving not just 6 pieces along the outside, but an extra one in the middle. I then tried to make 7 cuts by myself. I was successful.

I then tried to make 4 cuts. On my first try, I made 10 pieces being careful not to intersect with multiple lines at the same point. I was then interested in seeing what would happen if I cut the pie like a pizza, or into eights. I found that I was only able to make 8 pieces like this. I then discovered a new key point. When I cut, I must find the most number of sections to cut. This number is equal to the # of cuts. For example when I have a figure with 2 cuts and 4 sections, the third cut must pass through 3 of the sections, diving them into half. This makes those 3 sections double to 6, and you still have that uncut 1 section. I will now test my theory:

I started over with 1 cut. I then tried my formula. In order to have 2 cuts, I would need to divide 2 sections. I did and got four pieces. I then tried this again. In order to have 3 cuts, I take the previous result (4) and subtract the number of the cut (3), which before I found was equal to the number of sections the new cut must divide. Theses are the sections that do not change. I then take the number of the cut (3) and multiply it by 2, because when I divide a section, I cut it in half, doubling the number of sections. I then take the number of changed sections and add this to the number of unchanged sections. I find the total is 7, which is what I got before, and what the table on p. 421 says. This formula can be written as:

$4-3=1$

$3*2=6$

$1+6=7$

Or in words as:

$previous section - num of the cut = x$

$num of the cut * 2 = y$

$x + y = new num of sections$

Or simply as: $(4-3)+(3*2)$

I repeat this for having 4 pieces:

$7-4=3$

$4*2=8$

$3+8=11$

This is the same thing as I got before. I will try again for 5 pieces:

$11-5=6$

$5*2=10$

$6+10=16$

My next step is to verify this. After having a few bad tries in dividing sections on paper, I am finally able to follow the rule, and I find that my formula works.

My next step is to find a way to use sigma to make the equation. This was very difficult for me, because you must use the results of the equations as the basis for the next one or this is how to find 4 from scratch:

$([([(2-2)+(2*2)]-3)+(3+2)]-4)+(4*2)$

This will get quite crazy over time, and is complicated to write in a sigma.

$\sum_{x=2} (?-x)+(x*2)$

I was able to write this. X is equal to the number of cuts, and it only works on 2 or more cuts. The ? mark represents the previous result. Could I represent this with another sigma????

I worked on this for a bit, but then decided to move on. I thought that instead of the question mark, x would just be subtracted from 0, and when I add everything up again it would work. Sample for 4 cuts and equation for that:

$\sum_{x=2}-x+(x*2)$

$-2+(2*2)-3+(3*2)-4+(4*2)$

$-2+4-3+6-4+8$

$2+3+4$

$9$

This didn’t work either because of that -2. When I try for 3:

$-2+(2*2)-3+(3*2)$

$-2+4-3+6$

$2+3$

$5$

It is that darn -2. This may be because I am starting at x=2, maybe if I start at 1.

$\sum_{x=1}-x+(x*2)$

$-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)$

$-1+2-2+4-3+6-4+8$

$1+2+3+4$

$10$

I am 1 closer. What if I start at 0?

$\sum_{x=0}-x+(x*2)$

$-0+(0*2)-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)$

$-0+0-1+2-2+4-3+6-4+8$

$0+1+2+3+4$

$10$

This makes no difference; Why doesn’t it work????

I decide that I can just solve it by adding 1 to the sigma result:

$1+\sum_{x=1}-x+(x*2)$

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)$

$-1+2-2+4-3+6-4+8$

$0+0+1+2+8$

$11$

Yes! It works for 4, what about for 5. I just need to continue the sigma at the end.

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)$

$-1+2-2+4-3+6-4+8-5+10$

$0+0+1+2+8+5$

$16$

Yes works! Time to continue to 6, 7, 8, 9, and 10.

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)-6+(6*2)$

$-1+2-2+4-3+6-4+8-5+10-6+12$

$0+0+1+2+8+5+6$

$22$

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)-6+(6*2)-7+(7*2)$

$-1+2-2+4-3+6-4+8-5+10-6+12-7+14$

$0+0+1+2+8+5+6+7$

$29$

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)-6+(6*2)-7+(7*2)-8+(8*2)$

$-1+2-2+4-3+6-4+8-5+10-6+12-7+14-8+16$

$0+0+1+2+8+5+6+7+8$

$37$

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)-6+(6*2)-7+(7*2)-8+(8*2)-9+(9*2)$

$-1+2-2+4-3+6-4+8-5+10-6+12-7+14-8+16-9+18$

$0+0+1+2+8+5+6+7+8+9$

$46$

$1-1+(1*2)-2+(2*2)-3+(3*2)-4+(4*2)-5+(5*2)-6+(6*2)-7+(7*2)-8+(8*2)-9+(9*2)-10+(10*2)$

$-1+2-2+4-3+6-4+8-5+10-6+12-7+14-8+16-9+18-10+20$

$0+0+1+2+8+5+6+7+8+9+10$

$56$

As I continue along, I find that the numbers seem to go up as $\sum_{}x$ for some reason. Well there you are. I solved the POW.

Solution

1. In-Out Table:

# of Cuts	Max. # of pieces	Change
1	2
2	4	+2
3	7	+3
4	11	+4
5	16	+5
6	22	+6
7	29	+7
8	37	+8
9	46	+9
10	56	+10
$x$	$1+\sum_{x=1}-x+(x*2)$

2a. The numbers seem to go up as $\sum_{}x$ . Each time x is increased, the number goes up by whatever X is. However, $1+\sum_{x=1}x$ also works. This must be a simplified way to do it.

2b. 10 cuts = 56 pieces

3c. The explanation and example for finding 3 cuts the long way is: In order to have 3 cuts, I take the previous result (4, that is the result for 2 cuts) and subtract the number of the cut (3), which before I found was equal to the number of sections the new cut must divide. Theses are the sections that do not change. I then take the number of the cut (3) and multiply it by 2, because when I divide a section, I cut it in half, doubling the number of sections. I then take the number of changed sections and add this to the number of unchanged sections. I find the total is 7.

Simplified: When you divide it in half, you cut a certain # of sections in half, and keep some untouched. This keeps building and building.

3. $1+\sum_{x=1}-x+(x*2)$ or $1+\sum_{x=1}x$